Формулы и свойства логарифмов

Логарифм положительного числа b по основанию a (log_a b) — это показатель степени, в которую надо возвести a, чтобы получить b. b > 0, a > 0, а≠ 1.

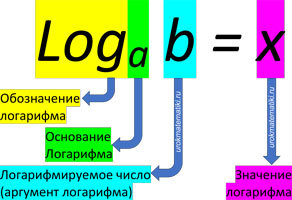
Для определения основания логарифма необходимо сначала определить его вид и, исходя из полученных результатов, по формуле и таблице сравнить корректность полученных значений. Это и будет основанием логарифма.

Чтобы решить логарифм необходимо понять, что a в степени x будет равно b, т.е. в какую степень x необходимо возвести основание логарифма a, чтобы получить значение b.

Примеры логарифмов:

В данных примерах можно увидель сложные и простые логарифмы, решение которых показывает, что всякий тождественный логарифм находится в пропорции его основания, за исключением вводных данных.

Конечно, основание логарифма пропорционально его значению, что приводит к равенству обратного значения. Это также необходимо учесть при рассмотрении равенства, кроме случаев, когда логарифм переностися с левой части равенства в правую.

${log}_{2}8=3$ (логарифм $8$ по основанию 2), так как $2^3=8$

${log}_{7}49=2$ (логарифм $49$ по основанию 7), так как $7^2=49$

${log}_5\frac{1}{5}=-1$ (логарифм $\frac{1}{5}$ по основанию 5), так как $5^{-1}=\frac{1}{5}$

Десятичный логарифм

Десятичный логарифм — логарифм по основанию 10.

Десятичный логарифм может быть не только как равенство степеней, но и показывать их различия. Наиболее хорошо это видно при разложении логарифма на члены в качестве констант a и b.

Конечным результатом решения десятичного логарифма является его сходство с натуральным логарифмом.

$lgb$ — десятичный логарифм (логарифм по основанию 10, $a=10$)

Примеры десятичных логарифмов:

$lg100=2$ — десятичный логарифм обозначается именно так (lg), это десятичный логарифм ста;

${log}_{10}100=2$ (другое обозначение десятичного логарифма), так как ${10}^2=100$. Но, строго говоря, это логарифм по основанию 10. Он будет иметь то же значение, что и десятичный логарифм.

Натуральный логарифм

При решении натурального логарифма его основа будет схожей с десятичным логарифмом за исключением того, что вместо числа 10 будет использоваться постоянная константа e.

Ещё одной особенностью натурального логарифма будет его неравенство по отношению к обратной функции.

Но стоит не приравнивать такое основание логарифма к прямой константе из-за большой разности при выборе метода подсчета логарифма.

$lnb$ — натуральный логарифм (логарифм по основанию e, $a=e$)

Можно провести аналогию с десятичным логарифмом, только здесь не число 10, а постоянная e; $e\approx 2.72$.

Основное логарифмическое тождество

Основание a, возведенное в степень логарифма с основанием a, будет равно b.

Логарифм единицы

Логарифмический ноль. Какое бы ни было основание логарифма, если в аргументе стоит 1, то логарифм всегда равен 0.

Вычисления такого логарифма применяются в балистике при расчете траектории движения объекта, находящегося в непосредственной близости от Земли. Это обусловлено наиболее точным значением ускорением свободного падения, равным 9,81. А при удалении от поверности Земли это значение изменяется, уменьшается пропорционально расстоянию удаления от поверхности.

Логарифм числа, равного основанию

Логарифмическая единица. Если аргумент и основание логарифма одинаковы, то значение логарифма будет равно единице.

Логарифм числа, обратного основанию

Если аргумент логарифма имеет значение обратное основанию, то значение логарифма будет равно -1.

Логарифм произведения двух положительных чисел

Сумма логарифмов. При умножении логарифмируемых чисел, можно сделать из них сумму 2-х логарифмов, у которых будут одинаковые основания.

Логарифм частного

Логарифм частного. При делении чисел мы получаем разность двух логарифмов с одинаковым основанием.

Логарифм степени положительного числа

Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа.

Логарифм корня числа

Логарифм корня равен частному от деления логарифма подкоренного числа на показатель корня.

Основание логарифма в степени

Формула перехода к новому основанию

Производная логарифма

Производная логарифмической функции по основанию равна единице, деленной на произведение подлогарифмической функции на натуральный логарифм основания.

При расчёте производной логарифма необходимо учитывать ложный коэффициент производной, при котором нарастает его гиперболическая составляющая. Это и есть главное условие корректного нахождения производной логарифма. В то же время, нельзя упускать второстепенные составляющие при расчёте. К ним относятся расчеты с применением общей суммы логарифмов, а также пропорциональная составляющая двух вычисляемых логарифмов. Такой подход можно применить не только для вычисления производной натурального логарифма, но и при расчете производной десятичного логарифма при возведении в степень x по основанию a.

y = log₂ x