Табличные значения синуса 30, 45, 60 градусов

Синус — это отношение противолежащего катета к гипотенузе.

синус 30 градусов
синус 45 градусов
синус 60 градусов

Синус 30 градусов

Необходимо найти синус 30 градусов.

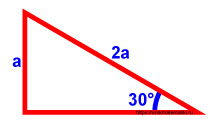
Напротив угла 30° находится катет, обозначим его как a.

В этом случае гипотенуза в два раза больше, так как катет, лежащий против угла 30° равен половине гипотенузы.

sin 30° = \frac{a}{2 a}

Сокращаем a:

sin 30° = \frac{a}{2 a} = \frac{1}{2}

Итак, $sin 30° = \frac{1}{2}$

Синус 45 градусов

Необходимо найти синус 45 градусов.

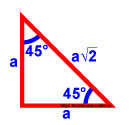
Если в прямоугольном треугольнике один угол равен 45°, то другой угол тоже равен 45° — получается равнобедренный треугольник. Обозначим стороны как a.

Синус — это отношение противолежащего катета к гипотенузе, но гипотенуза не известна. Найдём её по теореме Пифагора: сумма квадратов катетов, затем извлекаем корень.

\sqrt{2 a^{2}} = a \sqrt{2}

Так

sin 45° = \frac{a}{a \sqrt{2}}

Сокращаем a:

sin 45° = \frac{a}{a \sqrt{2}} = \frac{1}{\sqrt{2}}

Избавляемся от иррациональности, умножим числитель и знаменатель на $\sqrt{2}$ .

Итак, $sin 45° = \frac{\sqrt{2}}{2}$ — табличное значение.

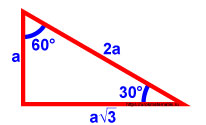
Синус 60 градусов

Необходимо найти синус 60 градусов.

Для этого рассмотрим треугольник из первого случая.

Так гипотенуза равна $2 a$ , а известный катет принят как a.

По теореме Пифагора можно найти катет, лежащий против угла 60°.

\sqrt{4 a^{2} - a^{2}} = \sqrt{3 a^{2}} = a \sqrt{3}

Находим синус 60° — отношение противолежащего катета к гипотенузе:

sin 60° = \frac{a \sqrt{3}}{2 a}

Сокращаем a:

sin 60° = \frac{a \sqrt{3}}{2 a}

Итак, $sin 60° = \frac{\sqrt{3}}{2}$

Коротко о важном
Таблицы
Формулы
Формулы по геометрии
Теория по математике

Натуральные числа.