Теорема о вписанном угле
Необходимо доказать, что вписанный угол равен половине дуги, на которую он опирается.
Существет три варианта расположения вписанного угла:
- вписанный угол проходит одной стороной через центр окружности
- центр окружности находится внутри вписанного угла
- центр окружности находится вне вписанного угла
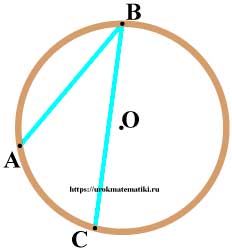
Вписанный угол проходит одной стороной через центр окружности
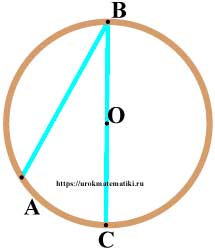
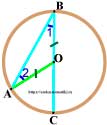
- Соедеиним точки O и A. Радиусы у окружности — одинаковые.
Это означает, что ∆ABO — равнобедренный, и ∠ 1 = ∠ 2. (У равнобедренного треугольника углы при основании равны.) - ∠ AOC — внешний для ∆AOB. А внешний угол равен сумме двух других несмежных с ним углов, ∠ AOC равен сумме ∠ 1 и ∠ 2. ∠ 1 и ∠ 2 — одинаковые.
А значит
А ∠ AOC — центральный и равен дуге.
Значит, угол ∠ 1 (∠ ABC) равен половине дуги AC:
Мы доказали: вписанный угол равен половине дуги, на которую он опирается.
Центр окружности находится внутри вписанного угла
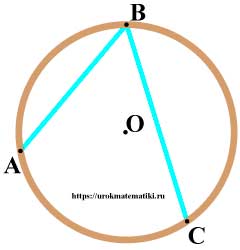
- Проведём луч BO, получим два угла (∠ 1 и ∠ 2), у которых одна сторона проходит через центр окружности.
Выше было доказано, что вписанный угол равен подовине дуги, на которую он опирается. Так
∠ 2 — тоже вписанный, у него одна сторона проходит через центр окружности. И тоже было доказано, что этот вписанный угол равен половине дуги, на которую он опирается.
- Теперь, если сложить ∠ 1 и ∠ 2 получится ∠ ABC.
Мы снова доказали, что вписанный угол равен половине дуги, на которую он опирается.
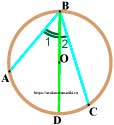
Центр окружности находится вне вписанного угла
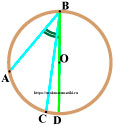
- Проведём луч BO.
В первом случае было доказано, что вписанный угол, у которого одна сторона проходит через центр, равен подовине дуги, на которую он опирается. Так - Ещё одни угол, сторона которого проходит через центр — ∠ CBD, тоже равен половине дуги, на которую он опирается.
- Теперь, если из большого угла ∠ ABD вычесть ∠ CBD получится ∠ ABC.
Для всех трёх случаев было доказано, что вписанный угол равен половине дуги, на которую он опирается.
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
