Минимум по геометрии 8 класса. Модуль 1
- четырёхугольник
- внутренние и внешние углы четырехугольника
- виды четырехугольников
- средняя линия треугольника
Четырёхугольник
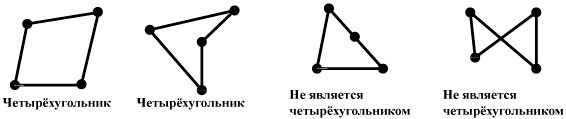
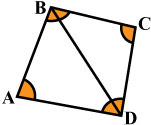
Четырёхугольник — это фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. При этом, никакие три из указанных точек не должны быть расположены на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырёхугольника, а соединяющие их отрезки - сторонами четырёхугольника.

Вершины, являющиеся концами одной стороны четырёхугольника, называются соседними, а вершины, не принадлежащие одной стороне — противолежащими. Стороны, имеющие общую вершину, называются соседними сторонами, а не имеющие общих вершин — противолежащими сторонами. Отрезки, соединяющие противолежащие вершины, называются диагоналями четырёхугольника. Точки, принадлежащие четырёхугольнику, делят плоскость q на два множества, которые образуют две области — внутреннюю и внешнюю.
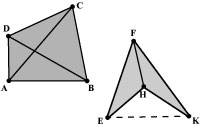
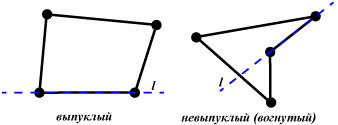
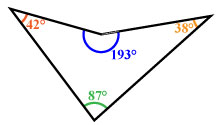
Если соединить любые две точки внутренней области выпуклого многоугольника, то отрезок, соединяющий эти точки, целиком находится во внутренней области четырёхугольника. Диагонали выпуклого четырёхугольника находятся во внутренней области. У невыпуклого четырёхугольника одна из диагоналей находится во внешней области. Каждая из двух диагоналей выпуклого четырёхугольника делит его на два треугольника.
Внутренние и внешние углы четырехугольника
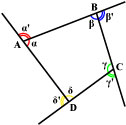
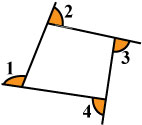
Угол, смежный любому углу выпуклого четырёхугольника, называется внешним углом. Из любой вершины четырёхугольника можно провести два внешних угла, которые являются вертикальными углами и соответственно равны друг другу. Поэтому, говоря о внешнем угле четырёхугольника, мы будем иметь в виду, один из них. На рисунке для внутренних углов α, β, γ, δ углы α', β', γ', δ' являются внешними.
Свойства сторон
- Каждая сторона четырехугольника меньше суммы всех его других сторон.
- Сумма диагоналей меньше его периметра.
Виды четырехугольников
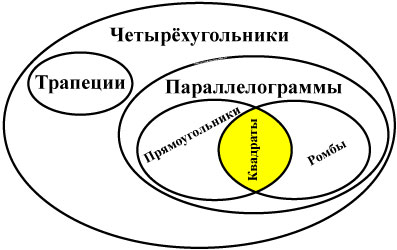
Параллелограмм
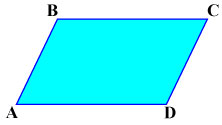
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма
- Противоположные стороны параллелограмма равны
- Противоположные углы параллелограмма равны
-
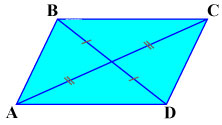 Диагонали параллелограмма точкой пересечения делятся пополам:
,
Диагонали параллелограмма точкой пересечения делятся пополам:
,
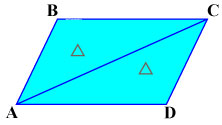 Диагональ делит параллелограмм на два равных треугольника: треугольники ABC и CDA равны.
Диагональ делит параллелограмм на два равных треугольника: треугольники ABC и CDA равны.- Сумма соседних углов равна 180°.
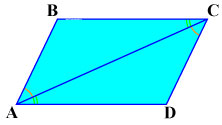 Накрест лежащие углы при диагонали равны: ,
Накрест лежащие углы при диагонали равны: , - Сумма всех углов равна 360°.
- Биссектриса отсекает от параллелограмма равнобедренный треугольник.
- Биссектрисы углов параллелограмма, прилежащих к одной стороне, взаимно перпендикулярны.
- Биссектрисы двух противолежащих углов параллелограмма параллельны.
- Периметр параллелограмма равен удвоенной сумме соседних сторон.
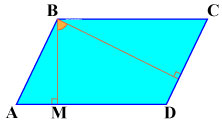 Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма.
Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма.
Признаки параллелограмма
- Две противоположные стороны одновременно равны и параллельны.
- Все противолежащие углы попарно равны.
- Все противоположные стороны попарно равны.
- Все противоположные стороны попарно параллельны.
- Обе диагонали в точке пересечения делятся пополам.
Прямоугольник
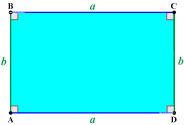
Прямоугольник — это четырехугольник, у которого все углы равны 90° (т.е. являются прямыми).
Если один угол параллелограмма прямой, то этот параллелограмм является прямоугольником.
Свойства прямоугольника
- Прямоугольник имеет все свойства параллелограмма.
- Все углы прямые.
- Диагонали прямоугольника равны.
- Периметр прямоугольника равен удвоенной сумме соседних сторон.
- При пересечении биссектрис внутренних углов произвольного параллелограмма образуется прямоугольник.
Признаки прямоугольников
- Если три угла четырёхугольника прямые, то этот четырёхугольник является прямоугольником.
- Если один угол параллелограмма прямой, то этот параллелограмм является прямоугольником.
- Если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником.
Ромб
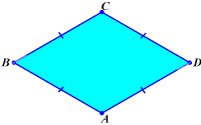
Ромб — это четырехугольник, у которого все стороны равны.
Ромб — это параллелограмм, у которого соседние стороны равны.
Свойства ромба
- Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма.
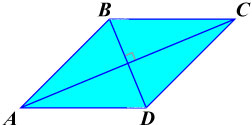 Диагонали ромба взаимно перпендикулярны: AC⊥BD.
Диагонали ромба взаимно перпендикулярны: AC⊥BD.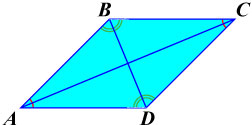 Диагонали ромба являются также биссектрисами его углов (делят углы ромба пополам).
Диагонали ромба являются также биссектрисами его углов (делят углы ромба пополам).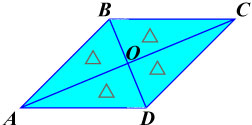 Диагонали делят ромб на четыре равных прямоугольных треугольника. Треугольники ABO, СBO, CDO, ADO — равные прямоугольные треугольники.
Диагонали делят ромб на четыре равных прямоугольных треугольника. Треугольники ABO, СBO, CDO, ADO — равные прямоугольные треугольники.
- Высоты ромба равны.
Признаки ромба
- Если диагонали параллелограмма перпендикулярны, то данный параллелограмм является ромбом.
- Если две смежные стороны параллелограмма равны, то данный параллелограмм является ромбом.
- Если диагонали параллелограмма являются биссектрисами его углов, то данный параллелограмм является ромбом.
- Если все стороны четырёхугольника равны, то данный четырёхугольник является ромбом.
Квадрат
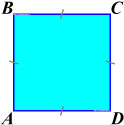
Квадрат — это это четырёхугольник, у которого все углы равны и все стороны равны.
Квадрат — это параллелограмм, у которого есть прямой угол и соседние стороны равны.
Квадрат — это прямоугольник, у которого соседние стороны равны.
Квадрат — это ромб, у которого есть прямой угол.
Свойства квадрата
- Квадрату присущи все свойства параллелограмма, прямоугольника и ромба.
 Диагонали квадрата делят его на четыре равных прямоугольных равнобедренных треугольника.
Диагонали квадрата делят его на четыре равных прямоугольных равнобедренных треугольника.
Признаки квадрата
- Если две смежные стороны прямоугольника равны, то этот прямоугольник является квадратом.
- Если диагонали прямоугольника перпендикулярны, то этот прямоугольник является квадратом.
- Если один из углов ромба прямой, то этот ромб является квадратом.
- Если диагонали ромба равны, то этот ромб является квадратом.
Средняя линия треугольника
Свойства
-
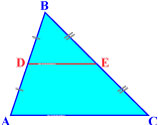
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
; -
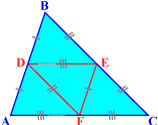
Три средних линии делят треугольник на 4 равных треугольника ADF, DBE, ECF, DEF.
-
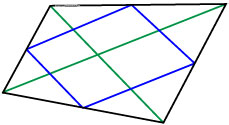
Середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.
-
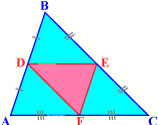
Средние линии треугольника образуют треугольник, периметр которого в два раза меньше периметра исходного треугольника.
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике