Формулы объема фигур

Объем фигуры — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

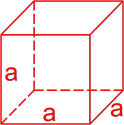
объём куба
объём призмы
объём параллелепипеда
объём прямоугольного параллелепипеда
объём пирамиды
объём цилиндра
объём конуса
объём шара

Объём куба

Куб — правильный многогранник, каждая грань которого представляет собой квадрат.

Объём куба равен кубу длины его грани.

V = a^{3}

где V — объем куба,
a - длина грани куба.

Объём призмы

Призма — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.

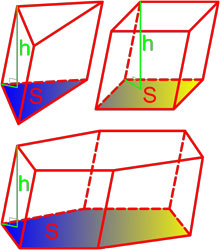
Объем призмы равен произведению площади основания призмы, на высоту.

Если в основании:

треугольник, то находите площадь треугольника,
квадрат, то — квадрата,
произвольная фигура, то найдите площадь произвольной фигуры.

V = S_{о} \cdot h

где V — объем призмы,
S_о — площадь основания призмы,
h — высота призмы — расстояние между её основаниями. Для прямой призмы, у которой все рёбра перпендикулярны основаниям — это любое из рёбер.

Объём параллелепипеда

Параллелепипед — многогранник, у которого шесть граней и каждая из них параллелограмм.

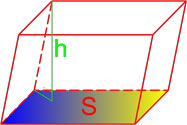
Объем параллелепипеда равен произведению площади основания параллелепипеда на высоту.

V = S_{о} \cdot h

где V — объём параллелепипеда,
S_о — площадь основания параллелепипеда,
h — высота параллелепипеда — расстояние между его основаниями.

Объём прямоугольного параллелепипеда

Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.

Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

V = a \cdot b \cdot h

где V — объём прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.

Объём пирамиды

Пирамида — это многогранник, основанием которого является произвольный многоугольник, а все грани представляют собой треугольники с общей вершиной, являющейся вершиной пирамиды.

Объём пирамиды с произвольным основанием

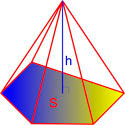
Объём пирамиды равен одной трети произведения площади основания на высоту.

V = \frac{1}{3} \cdot S \cdot h

где V — объём пирамиды,
S — площадь основания пирамиды,
h — высота пирамиды.

Объём усечённой пирамиды

Усеченная пирамида — часть пирамиды между ее основанием и этим сечением. Сечение параллельное основанию пирамиды делит пирамиду на две части.

Объём усеченной пирамиды равен одной трети произведения высоты h на сумму площадей верхнего основания S1, нижнего основания усеченной пирамиды S2 и средней пропорциональной между ними.

V = \frac{1}{3} \cdot h \cdot (S1 + \sqrt{S1 \cdot S2} + S2)

где V — объём усеченной пирамиды,
S1 — площадь верхнего основания усеченной пирамиды,
S2 — площадь нижнего основания усеченной пирамиды,
h — высота усеченной пирамиды.

Объём правильной пирамиды

Правильная пирамида — пирамида, в основани, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.

V = \frac{n \cdot a^{2} \cdot h}{12 \cdot tg \frac{180°}{n}}

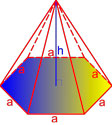где V — объём пирамиды,
a — сторона основания пирамиды,
n — количество сторон многоугольника в основании,
h — высота правильной пирамиды.

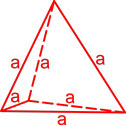
Объём правильной треугольной пирамиды

Правильная треугольная пирамида — пирамида, у которой основанием является равносторонний треугольник и грани — равные равнобедренные треугольники.

V = \frac{h \cdot a^{2}}{4 \cdot \sqrt{3}}

где V — объём правильной треугольной пирамиды,
a — сторона основания пирамиды,
h — высота правильной треугольной пирамиды.

Объём правильной четырёхугольной пирамиды

Правильная четырехугольная пирамида — пирамида, у которой основанием является квадрат и грани — равные равнобедренные треугольники.

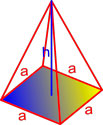
Объём правильной четырёхугольной пирамиды равен одной трети произведения высоты пирамиды на куб стороны основания пирамиды.

V = \frac{h \cdot a^{2}}{3}

где V — объём правильной четырёхугольной пирамиды,
a — сторона основания пирамиды,
h — высота правильной четырёхугольной пирамиды.

Объём тетраэдра

Тетраэдр — пирамида, у которой все грани — равносторонние треугольники.

Объем тетраэдра равен двенадцатой части произведения куба длины грани тетраэдра на квадратный корень из двух.

V = \frac{\sqrt{2}}{12} \cdot a^{3}

где V — объём тетраэдра,
a — любая из граней тетраэдра.

Объём цилиндра

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Объем цилиндра равен произведению площади его основания на высоту.

V = π \cdot R^{2} \cdot h = S \cdot h

где V — объём цилиндра,
S — площадь основания цилиндра,
R — радиус цилиндра,
π — число пи ≈ 3,14159265.

Объём конуса

Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.

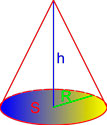
Объем конуса равен трети от произведения площади его основания на высоту.

V = \frac{1}{3} \cdot π \cdot R^{2} \cdot h = \frac{1}{3} \cdot S \cdot h

где V — объём конуса,
S — площадь основания конуса,
R — радиус основания конуса,
π — число пи ≈ 3,14159265.

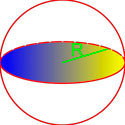
Объём шара

Шар — совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.

Объём шара равен четырём третьим от произведения числа пи на радиус шара в кубе.

V = \frac{4}{3} \cdot π \cdot R^{3}

где V — объём шара,
R — радиус шара,
π — число пи ≈ 3,14159265.

Коротко о важном
Таблицы
Формулы
Формулы по геометрии
Теория по математике

Натуральные числа.