Подготовка к контрольной работе по геометрии 8 класса

Свойства квадрата

1. Диагонали квадрата равны
2. Точка пересечения диагоналей делит их пополам
3. Диагонали квадрата взаимно перпендикулярны и делят его углы пополам

1. Площадь квадрата равна квадрату его стороны.
2. Равные фигуры имеют равные площади.
3. Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей многоугольников, из которых он состоит.
4. Площадь прямоугольника равна произведению смежных сторон; также можно сказать, что равна произведению длины на ширину.

Значения тригонометрических функций

1. $sin\mathrm{30°}=\frac{1}{2}$
   
   
2. $sin\mathrm{45°}=\frac{\sqrt{2}}{2}$
   
   
3. $sin\mathrm{60°}=\frac{\sqrt{3}}{2}$
   
   
4. $cos\mathrm{30°}=\frac{\sqrt{3}}{2}$
   
   
5. $cos\mathrm{45°}=\frac{\sqrt{2}}{2}$
   
   
6. $cos\mathrm{60°}=\frac{1}{2}$
   
   
7. $tan\mathrm{30°}=\frac{\sqrt{3}}{3}$
   
   
8. $tan\mathrm{45°}=1$
   
   
9. $tan\mathrm{60°}=\sqrt{3}$
   
   

В равностороннем треугольнике медиана является и биссектрисой, и высотой.

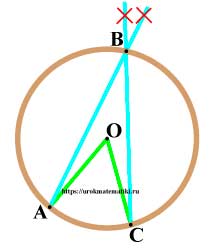
Вписанный (∠ABC) угол равен половине дуги, на которую он опирается, или половине центрального (∠AOC) угла.

Например, дуга (AC) — 80°, центральный равен дуге (тоже 80°), а вписанный угол — половине дуги (40°).

Коэффициент подобия — это отношение сходственных сторон.

Признаки подобия

1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы между ними равны, то такие треугольники подобны.
3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

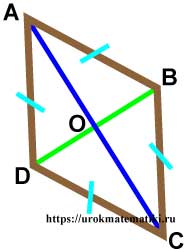
Свойства ромба

• Диагонали ромба (DB и AC) взаимно перпендикулярны и делят его углы пополам из-за того, что два треугольника (∆BDA и ∆BDC) равнобедренные.
• Так как ромб — это параллелограмм, то его диагонали (DB и AC) в точке пересечения (O) делятся пополам, а медиана является высотой и биссектрисой.