Тригонометрические формулы

Тригонометрические формулы — часто встречающиеся математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента.

тригонометрические функции
основные тригонометрические формулы
тригонометрические функции суммы и разности углов
тригонометрические функции двойного угла
формулы тройного угла
формулы понижения степени
формулы преобразования суммы и разности тригонометрических функций в произведение
формулы преобразования произведений функций
универсальная тригонометрическая подстановка

Тригонометрические функции

Синус

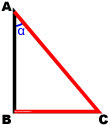
Синусом острого угла α в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.

sin α

Косинус

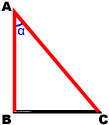
Косинусом острого угла α в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.

cos α

Тангенс

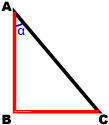
Тангенсом острого угла α в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.

tg α = \frac{sin α}{cos α}

α \neq \frac{π}{2} + π n

n є Z

Котангенс

Котангенсом острого угла α в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему катету.

ctg α = \frac{cos α}{sin α}

α \neq π + π n

n є Z

Секанс

Секанс — это тригонометрическая функция обратная косинусу.

sec α = \frac{1}{cos α}

α \neq \frac{π}{2} + π n

n є Z

Косеканс

Косеканс — это тригонометрическая функция обратная синусу.

cosec α = \frac{1}{sin α}

α \neq π + π n

n є Z

Основные тригонометрические формулы

{sin}^{2} α + {cos}^{2} α = 1

tg α \cdot ctg α = 1

1 + {tg}^{2} α = \frac{1}{{cos}^{2} α}

1 + {ctg}^{2} α = \frac{1}{{sin}^{2} α}

Тригонометрические функции суммы и разности углов

Синус суммы двух углов

sin (α + β) = sin α \cdot cos β + cos α \cdot sin β

Синус разности двух углов

sin (α - β) = sin α \cdot cos β - cos α \cdot sin β

Косинус суммы двух углов

cos (α + β) = cos α \cdot cos β - sin α \cdot sin β

Косинус разности двух углов

cos (α - β) = cos α \cdot cos β + sin α \cdot sin β

Тангенс суммы двух углов

tg (α + β) = \frac{tg α + tg β}{1 - tg α \cdot tg β}

Тангенс разности двух углов

tg (α - β) = \frac{tg α - tg β}{1 + tg α \cdot tg β}

Котангенс суммы двух углов

ctg (α + β) = \frac{ctg α \cdot ctg β - 1}{ctg β + ctg α}

Котангенс разности двух углов

ctg (α - β) = \frac{ctg α \cdot ctg β + 1}{ctg β - ctg α}

Тригонометрические функции двойного угла

Синус двойного угла

sin 2 α = 2 sin α \cdot cos α

Косинус двойного угла

cos 2 α = {cos}^{2} α - {sin}^{2} α

Тангенс двойного угла

tg 2 α = \frac{2 tg α}{1 - {tg}^{2} α}

Котангенс двойного угла

ctg 2 α = \frac{{ctg}^{2} α - 1}{2 ctg α}

Формулы тройного угла

Синус тройного угла

sin 3 α = 3 sin α - 4 {sin}^{3} α

Косинус тройного угла

cos 3 α = 4 {cos}^{3} α - 3 cos α

Тангенс тройного угла

tg 3 α = \frac{3 tg α - {tg}^{3} α}{1 - 3 {tg}^{2} α}

Котангенс тройного угла

ctg 3 α = \frac{3 ctg α - {ctg}^{3} α}{1 - 3 {ctg}^{2} α}

Формулы понижения степени

{sin}^{2} α = \frac{1 - cos 2 α}{2}

{cos}^{2} α = \frac{1 + cos 2 α}{2}

{sin}^{3} α = \frac{3 sin α - sin 3 α}{4}

{cos}^{3} α = \frac{3 cos α + cos 3 α}{4}

Формулы преобразования суммы и разности тригонометрических функций в произведение

sin α + sin β = 2 sin \frac{α + β}{2} \cdot cos \frac{α - β}{2}

sin α - sin β = 2 sin \frac{α - β}{2} \cdot cos \frac{α + β}{2}

cos α + cos β = 2 cos \frac{α + β}{2} \cdot cos \frac{α - β}{2}

cos α - cos β = - 2 sin \frac{α + β}{2} \cdot sin \frac{α - β}{2}

tg α + tg β = \frac{sin (α + β)}{cos α \cdot cos β}

tg α - tg β = \frac{sin (α - β)}{cos α \cdot cos β}

ctg α + ctg β = \frac{sin (α + β)}{sin α \cdot sin β}

ctg α - ctg β = \frac{sin (β - α)}{sin α \cdot sin β}

a sin α + b cos α = r sin (α + φ)

,

где

r^{2} = a^{2} + b^{2}

sin φ = \frac{b}{r}

tg φ = \frac{b}{a}

Формулы преобразования произведений функций

sin α \cdot sin β = \frac{cos (α - β) - cos (α + β)}{2}

sin α \cdot cos β = \frac{sin (α + β) + sin (α - β)}{2}

cos α \cdot cos β = \frac{cos (α + β) + cos (α - β)}{2}

Универсальная тригонометрическая подстановка

sin α = \frac{2 tg \frac{α}{2}}{1 + {tg}^{2} \frac{α}{2}}

cos α = \frac{1 - {tg}^{2} \frac{α}{2}}{1 + {tg}^{2} \frac{α}{2}}

tg α = \frac{2 tg \frac{α}{2}}{1 - {tg}^{2} \frac{α}{2}}

ctg α = \frac{1 - {tg}^{2} \frac{α}{2}}{2 tg \frac{α}{2}}

Коротко о важном
Таблицы
Формулы
Формулы по геометрии
Теория по математике

Натуральные числа.