Теорема Пифагора
Теорема Пифагора — пожалуй, одна из самых известных теорем в математике вообще и геометрии в частности. На самом деле несмотря на то, что она названа именем Пифагора, она была известна еще за тысячу лет до него.
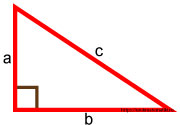
Терема Пифагора гласит следующее: если у нас есть прямоугольный треугольник с катетами a, b и гипотенузой c, то сумма квадратов катетов равна квадрату гипотенузы.
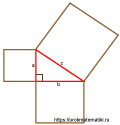
Мы знаем, что величина описывает площадь квадрата со стороной a. То есть, если мы на катете a построим квадрат, на катете b построим квадрат и на гипотенузе c построим квадрат, мы получим, что площадь квадрата со стороной a + площадь квадрата со стороной b равняется площади квадрата со стороной c. Это, так называемое, геометрическое объяснение теоремы Пифагора: сумма площадей квадратов, построенных на катетах, равняется площади квадрата построенного на гипотенузе.
Если вы построите вместо квадратов любые подобные фигуры, допустим полуокружности, то сумма этих площадей, построенных на катетах, все равно будет равняться площади фигуры, построенной на гипотенузе.
Доказательство теоремы Пифагора
На сегодняшний день известно более 200 различных доказательств теоремы Пифагора. Мы воспользуемся одним из них.

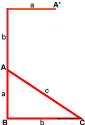
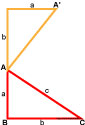
Для того, чтобы доказать теорему Пифагора, мы рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой c.
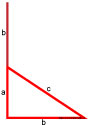
Достроим прямоугольный треугольник со сторонами a, b, c до квадрата следующим образом: катет длиной a мы достраиваем на расстояние b.
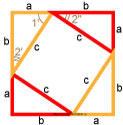
Мы знаем:
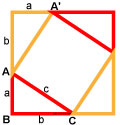
- Площадь квадрата со стороной a+b равна квадрату стороны (a+b).
- Квадрат состоит их четырех одинаковых прямоугольных треугольников и внутренней фигуры — квадрата. Площадь каждого прямоугольного треугольника — половина произведения его катетов.
- Внутренняя фигура — квадрат имеет стороны c.
Докажем, что внутренняя фигура — это квадрат.
У фигуры все стороны равны — значит это ромб. Если доказать, что один угол является прямым, то все остальные углы будут прямыми.
Из свойств прямоугольного треугольника мы знаем, что острые углы прямоугольного треугольника равны 90°.
Т.к. все показанные треугольники равны, то и
Отсюда следует, что — это угол между сторонами внутренней фигуры — ромба.
В нашем случае было доказано, что этот ромб является квадратом.
Преобразовав описанное выше в формулу, получаем:
Раскроем формулу квадрата суммы:
Сокращаем 2ab:
Получаем:
Мы доказали теорему Пифагора.
Задачи на тему "Теорема Пифагора"
Египетский треугольник
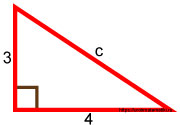
Дано:
Прямоугольный треугольник с катетами 3 и 4.
Требуется найти его гипотенузу.
Решение:
Обозначим гипотенузу как c и воспользуемся теоремой Пифагора: сумма квадратов катетов равняется квадрату гипотенузы:
Ответ: гипотенуза прямоугольного треугольника с катетами с катетами 3 и 4 равна 5.
Прямоугольный треугольник со сторонами 3, 4 и 5 называется египетским.
Пифагорова тройка
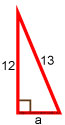
Дано:
Гипотенуза равна 13, а один из катетов равен 12.
Требуется найти второй катет.
Решение:
Обозначим второй катет как a и снова воспользуемся теоремой Пифагора: сумма квадратов катетов равняется квадрату гипотенузы:
Ответ: второй катет a прямоугольного треугольника с гипотенузой 13 и одним из катетов 12 равен 5.
Обратите внимание, что в первом и втором примерах стороны треугольников получились целыми числами. Такие числа, которые удовлетворяют теореме Пифагора, называются пифагоровыми тройками.
Равнобедренная трапеция
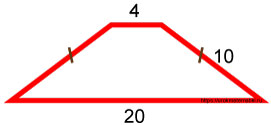
Дано:
Равнобедренная трапеция. Верхнее основание равно 4, боковая сторона равна 10, нижнее основание равно 20.
Требуется найти площадь трапеции S.
Решение:
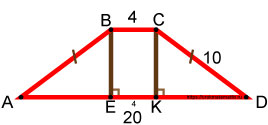
Обозначим углы трапеции точками A, B, C, D. Из точек B и C опустим перпендикуляры на сторону AD в точки E и K соответственно.
Рассмотрим четырёхугольник BCKE. Этот четырёхугольник является прямоугольником. Стороны BC и EK взаимно параллельны, и стороны BE и CK тоже взаимно параллельны, причём один из углов прямоугольника BCKE имеет 90°. Это доказывает, что прямоугольник BCKE является прямоугольником.
В прямоугольнике противоположные стороны равны. Если отрезок BC равен 4, то EK тоже равен 4.
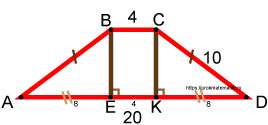
Так как наша трапеция равнобокая, то левый и правый треугольники равны между собой, т.к. имеют одинаковые катеты и одинаковые гипотенузы. По признакам равенства прямоугольных треугольников они равны. Это означает, что отрезки AE и KD равны между собой.
Отрезок AD равен 20, отрезок EK равен 4. Значит, на отрезки (AE+KD) остаётся . Значит, каждый из них равен 8.
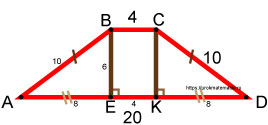
Рассмотрим любой из треугольников, например, ABE. Он является прямоугольным. Один из катетов равен 8, а гипотенуза равна 10.
По теореме Пифагора можем найти BE. Сумма квадратов катетов равна квадрату гипотенузы:
Таким образом мы нашли высоту трапеции.
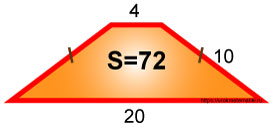
Теперь можно найти площадь трапеции S.
Площадь трапеции равна полусумме оснований умноженной на высоту трапеции.
Ответ: площадь трапеции S равна 72.
Применение теоремы Пифагора
Наиболее частое применение теоремы Пифагора можно увидеть в строительстве. В современные дальномеры встраивается функция, косвенно определяющая размеры стороны (треугольника) при измерении двух других сторон.
Рассмотрим два теоретических примера, когда необходимо произвести расчёт конструкции крыши, а в другом примере научимся позиционировать стены дома относительно друг друга под углом 90°.
Расчет стропильной системы крыши
Задача крайне упрощённая для точных расчётов стропильной системы крыши, но достаточно понятная, чтобы донести принципы расчёта по теореме Пифагора.
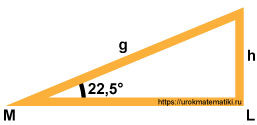
Дано:
Расстояние между мауэрлатом (M) и лежнем (L) (они лежат на стенах) известно и равно 5 метрам.
Крыша покрыта металлочерепицей, минимальный рекомендуемый угол наклона которой является 22,5°.
Стойка (h) расположена строго перпендикулярно лежню (L)
Требуется найти длину стропила (g) и высоту стойки (h).
Решение:
Чтобы найти высоту стойки (h) можно применить теорему синусов. Для этого необходимо найти угол, который лежит против известной стороны. Зная, что сумма углов треугольника равна 180° вычисляем угол, лежащий против известной стороны ML
Теперь подставляем в формулу известные значения для определения высоты стойки (h) по теореме синусов:
Также по теореме синусов можно найти и длину (g), но нас интересует теорема Пифагора.
Поэтому зная, что квадрат гипотенузы (в нашем случае это g) равен сумме квадратов катетов (в нашем случае это h и расстояние между точками ML), получаем:
Подставляя в формулу ранее вычисленные и известные значения, получаем:
Ответ: полученные значения исчисляются в метрах. В строительстве округление до миллиметров таких деталей — более чем точно. Поэтому округляя значения стропилы g и стойки h, получаем:
мм
мм
Египетский треугольник
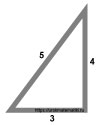
Ещё одним примером практического применения теоремы Пифагора в строительстве может служить использование египетского треугольника.
Чтобы на плоской поверхности вывести угол 90°, необходимо взять верёвку и отложить на ней три расстояния: 3, 4, 5. И не важно в каких единицах измерения будут отрезки, возможно эти единицы измерения будут выдуманными вами.
Соедините верёвку в треугольник, как показано на изображении, и натяните стороны полученного треугольника.
Угол между сторонами 3, 4 всегда будет равен 90°. По нему можно разметить стены или фундамент будущего дома.
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике