Формулы площадей фигур
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
- формулы площади треугольника
- формулы площади квадрата
- формула площади прямоугольника
- формулы площади параллелограмма
- формулы площади ромба
- формулы площади трапеции
- формулы площади дельтоида
- формулы площади произвольного выпуклого четырехугольника
- формулы площади круга
- формула площади эллипса
Формулы площади треугольника
Формулы — это не только способ вычисления, но и ключ к пониманию мира вокруг нас.
Однажды в университете на лекции по геометрии профессор рассказал студентам о формуле площади треугольника.
"Итак, друзья мои, - начал он, - если у вас есть треугольник со сторонами a, b и c, то его площадь можно вычислить по формуле S = (a * b * c) / (4 * h), где h - высота треугольника, проведенная к одной из сторон."
Студенты начали записывать формулу в свои тетради, но один из них, по имени Алексей, решил проверить ее на практике. Он взял лист бумаги, нарисовал треугольник и начал измерять его стороны и высоту.
Когда он закончил измерения, он подставил все значения в формулу и получил результат: S = 22,5 см².
Однако когда он проверил свой ответ на калькуляторе, то обнаружил, что он ошибся в вычислениях и получил неверный результат.
Он попытался понять, где он допустил ошибку, и заметил, что в формуле не хватает одного знака. Оказалось, что вместо "h" нужно было написать "h²", чтобы получить правильный результат.
С тех пор Алексей стал более внимательным при изучении формул и всегда проверял их правильность перед использованием. И он понял, что иногда даже самые простые формулы могут быть сложными для понимания, если не знать всех деталей.

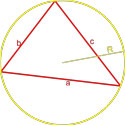
Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
,где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.
Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c.
,где p — полупериметр треугольника:
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
,где a, b — стороны треугольника,
γ — угол между сторонами a и b.
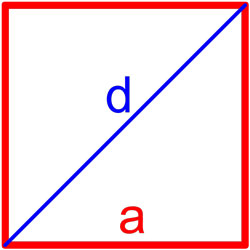
Формулы площади квадрата
Альберт Эйнштейн и формула площади квадрата
 Однажды, в одном городе, жил-был ученый по имени Альберт Эйнштейн. Он был известен своими открытиями в области физики и математики, но однажды он столкнулся с проблемой, которая казалась ему неразрешимой.
Однажды, в одном городе, жил-был ученый по имени Альберт Эйнштейн. Он был известен своими открытиями в области физики и математики, но однажды он столкнулся с проблемой, которая казалась ему неразрешимой.
Однажды Альберт решил провести эксперимент, чтобы доказать свою теорию о том, что площадь квадрата равна квадрату его длины. Но как он ни старался, он не мог найти способ, как это сделать. Он провел множество экспериментов, использовал различные методы и инструменты, но все было напрасно.
В конце концов, он решил обратиться за помощью к своим коллегам-ученым. Когда он пришел к ним, они были удивлены его просьбой. Они сказали ему, что это невозможно, потому что площадь квадрата не может быть выражена в виде формулы. Но Альберт не сдавался. Он продолжал искать решение этой проблемы.
И однажды, когда он сидел в своем кабинете, его осенило. Он понял, что площадь квадрата можно выразить в виде формулы, если использовать не длину стороны квадрата, а его диагональ. И вот, наконец, Альберт нашел решение своей проблемы. Он создал формулу, которая позволяла вычислить площадь квадрата по его диагонали. Это было настоящим прорывом в науке!
С тех пор Альберт стал известен как создатель формулы площади квадрата. Его открытие стало одним из самых важных в истории математики и физики.
Формула площади прямоугольника
Жил-был учёный, который не мог запомнить формулу...
Жил-был один ученый по имени Иван Иванович. Он был очень умный и талантливый, но у него была одна проблема — он не мог запомнить формулы.
Однажды ему нужно было вычислить площадь прямоугольника, и он начал думать: "Площадь прямоугольника равна длине умноженной на ширину". Но как только он начинал писать формулу, его мысли разбегались, и он забывал, что хотел написать.
Тогда Иван Иванович решил пойти к своему другу, который был математическим гением. Он спросил у него, как вычислить площадь прямоугольника. Друг ответил: "Площадь прямоугольника равна удвоенной длине на ширину". Иван Иванович был очень удивлен, ведь он всегда думал, что площадь равна длине умножить на ширину. Но друг объяснил ему, что если мы удвоим длину, то получим удвоенную площадь, а если удвоим ширину, то получим утроенную площадь.
С тех пор Иван Иванович стал запоминать формулы с помощью картинок. Он рисовал прямоугольник на бумаге, а затем делил его на две части и рисовал еще один прямоугольник внутри первого. Затем он писал формулу площади для каждого прямоугольника и соединял их вместе. Теперь Иван Иванович мог легко вычислять площадь прямоугольника и не забывать формулы. И он понимал, что это не только помогает ему в учебе, но и делает его более умным и сообразительным.
Формулы площади параллелограмма
Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.
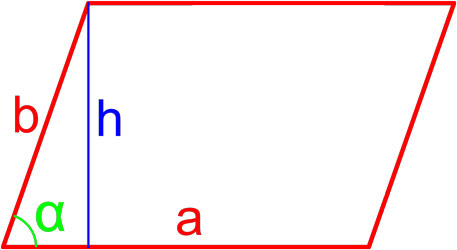
Формула площади параллелограмма по длине стороны и высоте

Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
,где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.
Формула площади параллелограмма по двум сторонам и углу между ними

Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
,где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α - угол между сторонами параллелограмма.
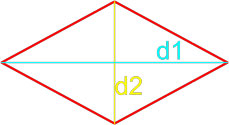
Формула площади параллелограмма по двум диагоналям и углу между ними
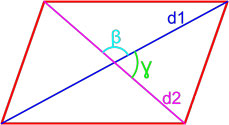
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
,где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β, γ - угол между диагоналями параллелограмма.
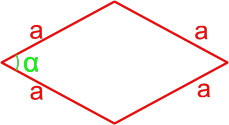
Формулы площади ромба
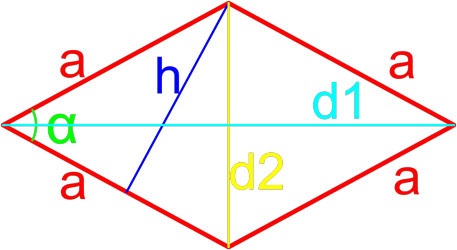
Формула площади ромба по длине стороны и высоте
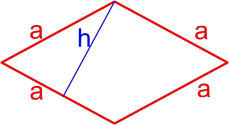
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
,где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.
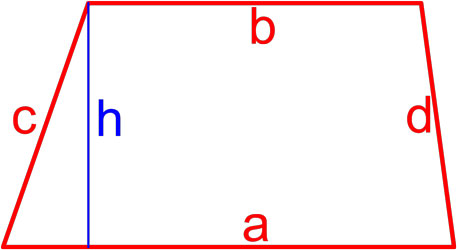
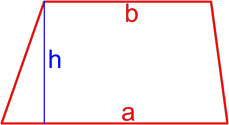
Формулы площади трапеции
Трапеция — это четырёхугольник, у которого две (a, b) стороны параллельны (основания), а две другие (c, d) стороны не параллельны (боковые стороны).
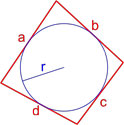
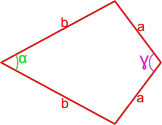
Формулы площади дельтоида
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.
Формула площади дельтоида по двум неравным сторонам и углу между ними
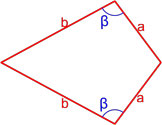
Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.
,где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.
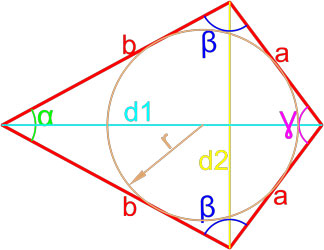
Формула площади дельтоида по равным сторонам и углу между ними
Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.
,где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b,
γ — угол между равными сторонами a.
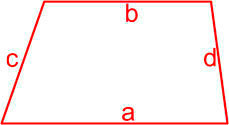
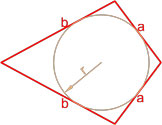
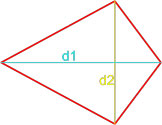
Формулы площади произвольного выпуклого четырехугольника
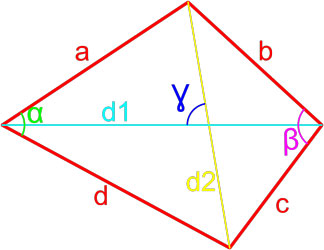
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
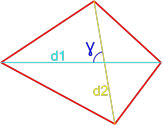
Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.
,где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.
Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
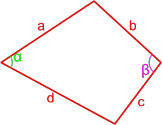 ,
,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
— полупериметр четырехугольника,
— полусумма двух противоположных углов четырехугольника.
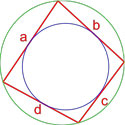
Формула площади вписанного четырехугольника (формула Брахмагупты)
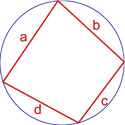
Если вокруг четырехугольника можно описать окружность, то его площадь равна
,где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
— полупериметр четырехугольника.
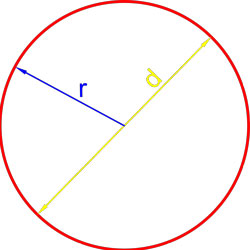
Формулы площади круга
Площадь сегмента круга
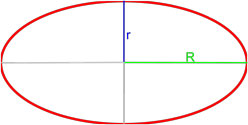
Формула площади эллипса
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике