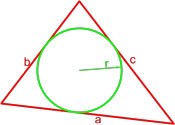
Треугольник
Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.

- типы треугольников
- вершины углы и стороны треугольника
- медианы треугольника
- биссектрисы треугольника
- высоты треугольника
- окружность вписанная в треугольник
- окружность описанная вокруг треугольника
- связь между вписанной и описанной окружностями треугольника
- средняя линия треугольника
- периметр треугольника
- формулы площади треугольника
- равенство треугольников
- подобие треугольников
- прямоугольные треугольники
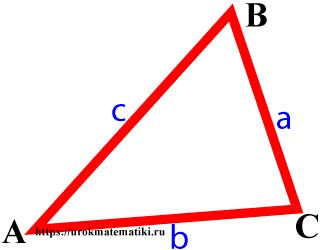
Вершины, углы и стороны треугольника
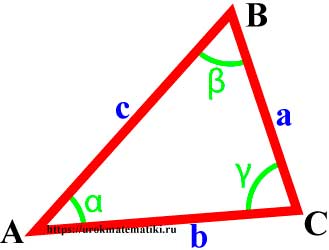
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы
- если , тогда
- если , тогда
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.
Теорема о проекциях
Для остроугольного треугольника:
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианы
Медианы треугольника
Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
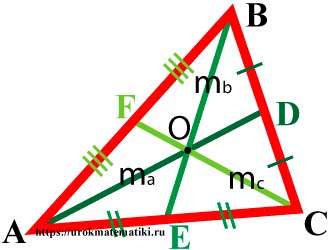
Свойства медиан треугольника
- Медианы треугольника пересекаются в одной точке. Точка пересечения медиан называется центроидом.
- В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
- Медиана треугольника делит треугольник на две равновеликие части
- Треугольник делится тремя медианами на шесть равновеликих треугольников
- Из векторов, образующих медианы, можно составить треугольник
Формулы медиан треугольника
Формулы медиан треугольника через стороны
Биссектрисы треугольника
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
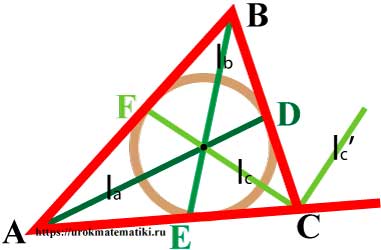
Свойства биссектрис треугольника
- Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, - центре вписанной окружности.
- Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
- Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°
Угол между и - Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны
где — полупериметр треугольника.
Формулы биссектрис треугольника через две стороны и угол
Высоты треугольника
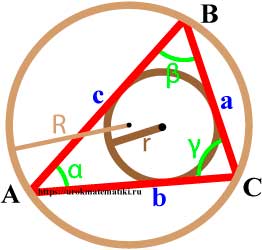
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться:
- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
- Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
- Если в треугольнике две высоты равны, то треугольник — равнобедренный.
Формулы высот треугольника
Формулы высот треугольника через сторону и угол
Формулы высот треугольника через сторону и площадь
Формулы высот треугольника через две стороны и радиус описанной окружности
Окружность вписанная в треугольник
Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
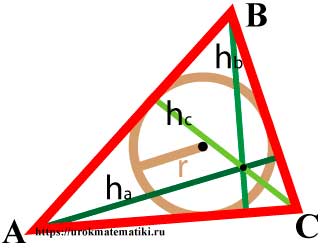
Свойства окружности вписанной в треугольник
- Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
- В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру
Радиус вписанной в треугольник окружности через три стороны
Формулы высот треугольника через две стороны и радиус описанной окружности
Окружность описанная вокруг треугольника
Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
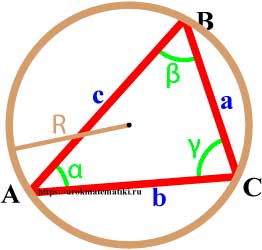
Свойства окружности описанной вокруг треугольника
- Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
- Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь
Радиус описанной окружности через площадь и три угла
Радиус описанной окружности через сторону и противоположный угол (теорема синусов)
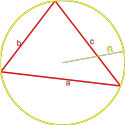
Связь между вписанной и описанной окружностями треугольника
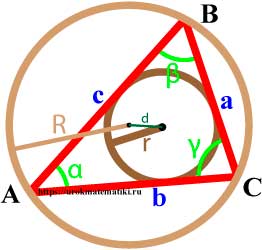
Формулы радиуса окружности описанной вокруг треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то
Радиус описанной окружности через площадь и три угла
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
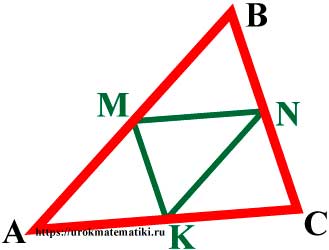
Свойства средней линии треугольника
- Любой треугольник имеет три средних линии.
- Средняя линия треугольника параллельна основанию и равна его половине.
; ;
; ; - Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольника.
; ; - При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
;
;
;
Признаки
Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Формулы площади треугольника
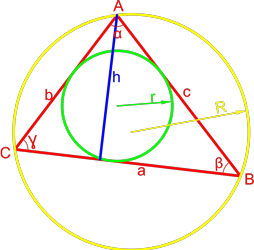
Формула площади треугольника по стороне и высоте
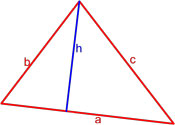
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
,
,
,
где a, b, c — стороны треугольника,
ha, hb, hc — высоты, проведенные к сторонам a, b, c треугольника.
Формула площади треугольника по трем сторонам
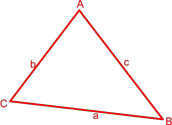
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c.
,где p — полупериметр треугольника:
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
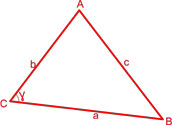
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
,
,
,
где a, b, c — стороны треугольника,
γ — угол между сторонами a и b,
α — угол между сторонами b и c,
β — угол между сторонами a и c.
Равенство треугольников
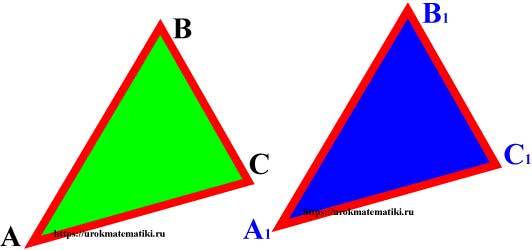
Определение
Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства
У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).
Признаки равенства треугольников
По двум сторонам и углу между ними
Теорема.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
По стороне и двум прилежащим углам
Теорема.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
По трем сторонам
Теорема.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Подобие треугольников
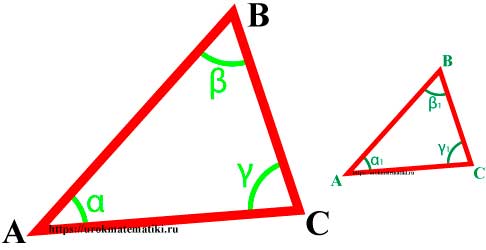
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
,, и
где k — коэффициент подобия.
Признаки подобия треугольников
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Прямоугольные треугольники
Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).
Свойства прямоугольного треугольника
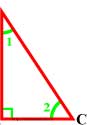 Сумма двух острых углов прямоугольного треугольника равна 90°.
Сумма двух острых углов прямоугольного треугольника равна 90°.
Сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника .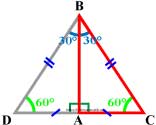
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).
Рассмотрим прямоугольный треугольник ABC, в котором ∠ A — прямой, ∠ B = 30°, и значит, что ∠ C = 60°.
Докажем, что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD , как показано на рисунке.
Получим треугольник BCD, в котором ∠ B = ∠ D = 60° , поэтому DC = BC. Но DC = 2AC. Следовательно, BC = 2AC.Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.
Признаки равенства прямоугольных треугольников
Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике